密码学复习

任课老师：白洪欢

前期知识

数学基础

gcd相关定理

设a,b为整数且至少有一个不为0, 令d = gcd(a,b), 则一定存在整数x, y 有:

特别的,当a,b互素时一定存在整数x，y使得 上述的右式为1成立

扩展欧几里得法

对于一个整数a来说，如果它存在模n的乘法逆元 , 那么这一充分必要条件是， a与n是互素的

素数相关的定理

任意大于0的整数 都能唯一分解成素数的乘积：

古典密码

• 频率分析表可以对付单表密码
• 仿射密码
  • 以加密为例：

Vigenere

Vigenere是一种多表简单加法密码.

• 明文为 m1,m2…mp; 密钥为 k1,k2…kq
• 当q小于p时, 重复使用密钥;
• 加密:
• 解密:

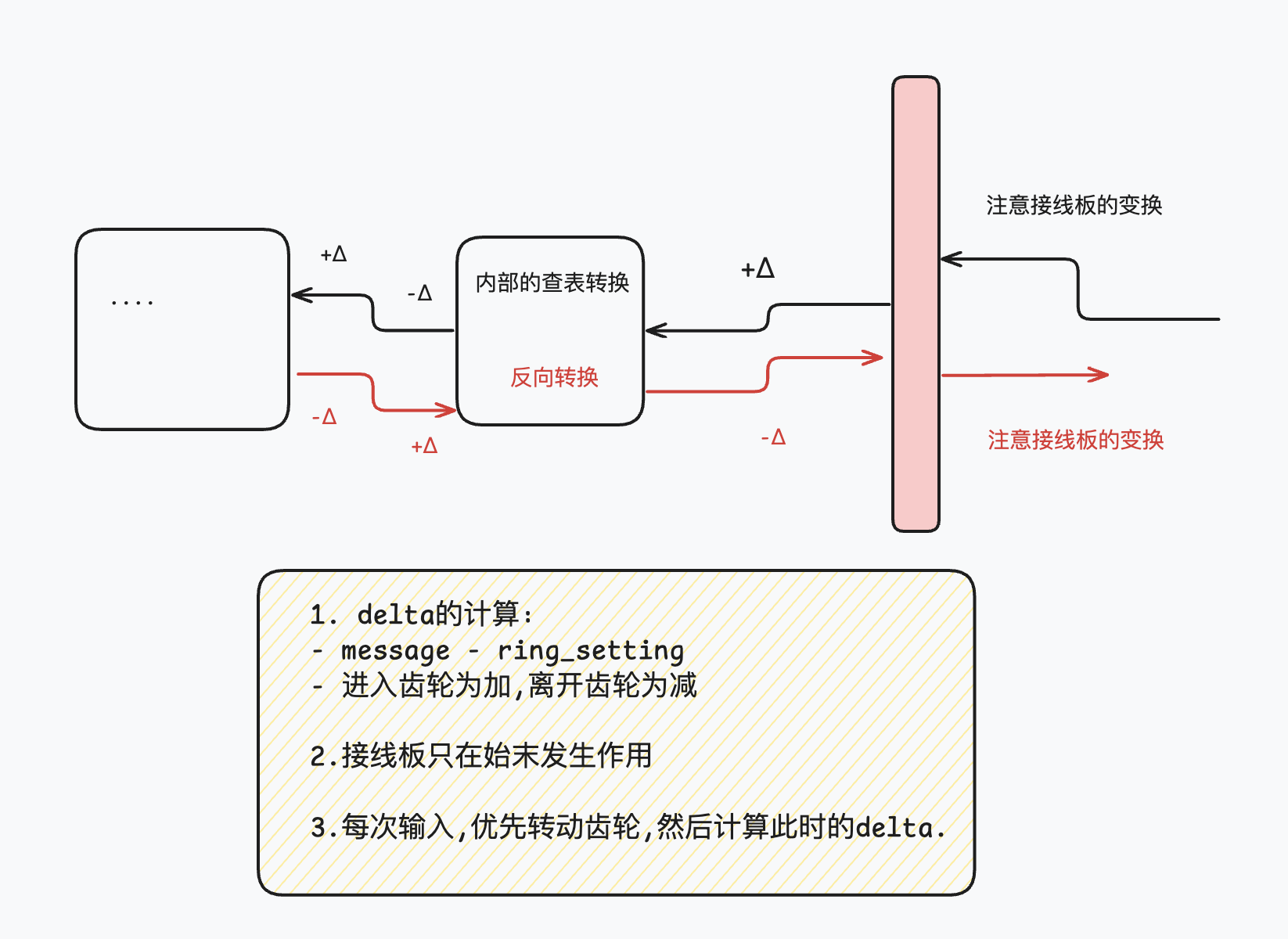
Enigma

流程图：

Hash函数

MD5

使用～加密的过程也被称作生成摘要的过程，相当于有损压缩

• 报文的长度固定为128位

md5是一种单向函数，意味着可能有多个输入对应相同的输出

• 如果不同的报文计算得到的摘要相同，就称为发生了碰撞 collision

分块与填充

• 如果最后一块的大小正好是64字节，还需要额外填充一块
• 1字节的 0x80以及8字节的 count 是一定要填充的
• 按照最后一块的大小，分为小于56与介于56和63字节之间2种情况

源代码分析

结构体

typedef struct _MD5_CTX
{
   ulong32  state[4]; /* 128位摘要 */
   ulong32  count[2]; /* 已处理的报文的二进制位数,最大值=2^64-1 */
   unsigned char  data[64]; /* 64字节message块 */
} MD5_CTX;

此处的count计数的是比特位而不是字节！因此通过下面的方式计算字节数：

bytes_left = (MD5_ctx->count[0] >> 3) & 0x3F;

&0x3F 等价于 %64 也就是 和 n-bit的1进行与计算，相当于 mod

Update

每次不断向其中添加新数据，添加前需要补充的字节数如果小于buf_len，说明可以补齐为1个block来处理，否则进入else分支直接赋值

Final

int Final_MD5(MD5_CTX *MD5_ctx)
{
   ulong32 bytes_left, pad_len;
   unsigned char total_bits[8];

   // unsigned char * 进行强制类型转换, 使得8“位”实际上得到的是64bits, 也就是计数的全部内容.
   
   memcpy(total_bits, (unsigned char *)MD5_ctx->count, 8); // total_bits=
                                                           // 已处理的报文的二进制位数
                                                           // (含data中剩余的字节)
                                                           // 后面补充的pad_stuff及
                                                           // total_bits本身不计在内
   bytes_left = (MD5_ctx->count[0] >> 3) & 0x3F;
   pad_len = (bytes_left < 56) ? (56 - bytes_left) : 
               (64 - bytes_left + 56); // bytes_left==56时, 要补8+56=64字节
                                       // bytes_left==57时, 要补7+56=63字节
   Update_MD5(MD5_ctx, pad_stuff, pad_len); // 把pad_stuff加到data中计算
   Update_MD5(MD5_ctx, total_bits, 8); // 把total_bits加到data中计算
   return 0;
}

• 注意 pad_len在此处就是填充值的字节数，按照最后一个块的字节数的56划分
• count中，不包含填充值和本身，只是计数处理的字节数

彩虹表破解MD5

以4个大写字母的彩虹表为例:

1. 生成随机数 n [0, ], 得到对应的字母

   比如 AAAA 对应 0

2. 计算

   1. 每次将得到的 取模得到上述的 , 循环计算, 得到最后的一个 ;
   2. 记录循环序列初始的 n与最后的 m.

3. 循环上述操作 k 次, 得到 k对的值存入数据库, 然后用报文 在数据库当中检索 m.

4. 如果立即找到, 说明是这对键值对的 , 使用 重新计算即可.

5. 如果在数据库中找不到 的值, 作以下的操作

   如果此时的 在数据库中存在, 那么说明此时的 就是那一对 n与m计算序列中的 所对应的 .

   如果继续找不到, 那么就循环上述的步骤.

NOTICE：

• 生成一个随机数的之后，计算其MD5值 , 然后将其赋值给 （注意需要取模处理），迭代计算， 直至索引为100， 因此最后一个随机数计算得到的链上有101个MD5值
• 数据库中只存储一开始的随机数（为了开始计算），以及链尾的MD5值（为了查询比较）
• 如果初始的100个md5的值中存在对应的，就认为明文是对应的 (然后转换为字母组合)；
• 如果一开始查询不到，就按照下面的说法继续计算：

注意，是向前迭代，也就是说存储的都是0和100，比较的都是idx=100的md5值

SHA

• sha-1得到的hash值是160位 = 20 字节
  • 使用5个32位寄存器
• ～也是分块计算，每块64字节，不足64字节时按照与md5相同的方法填充

结构体

typedef struct _SHA1_CTX 
{
   ulong state[5];    // 5个32位寄存器，对应A,B,C,D,E
   struct {ulong hi, lo;} length;  // 64位消息长度计数器
   uchar data[64];    // 512位的消息块
} SHA1_CTX;

ROL

循环左移

static ulong ROL(ulong x, int number) /* left circular shift number bits */
{
   return (x << number) | (x >> (32 - number));
}

在低位进行或运算，补充之前移出的位

• BigEndian 将buf中的long转换成大端的存储格式
• final中：

  BigEndian(digest, 20); 
  /*[%] 注意SHA1的hash值共5个state, 每个state为ulong类型, 
        输出的时候,不可以把5个state当作连续的20个字节并以
        字节为单位按从左到右顺序输出, 而应该以ulong为单位
        分5次输出. 这是因为在Little-Endian的机器中, ulong
        是按低字节在前高字节在后的顺序存放在内存中的 , 若
        以字节为单位输出ulong , 则从左到右输出的4个字节与
        直接输出ulong所得的4字节顺序刚好是反的.
        这里为了达到以字节为单位按从左到右顺序输出的目的,
        特地调用BigEndian()这个函数对每个ulong所包含的4个
        字节颠倒顺序, 这样一来,  digest中包含的20字节摘要
        就可以按从左到右顺序输出了.
  */
  #endif

分组密码工作与流密码

分组密码

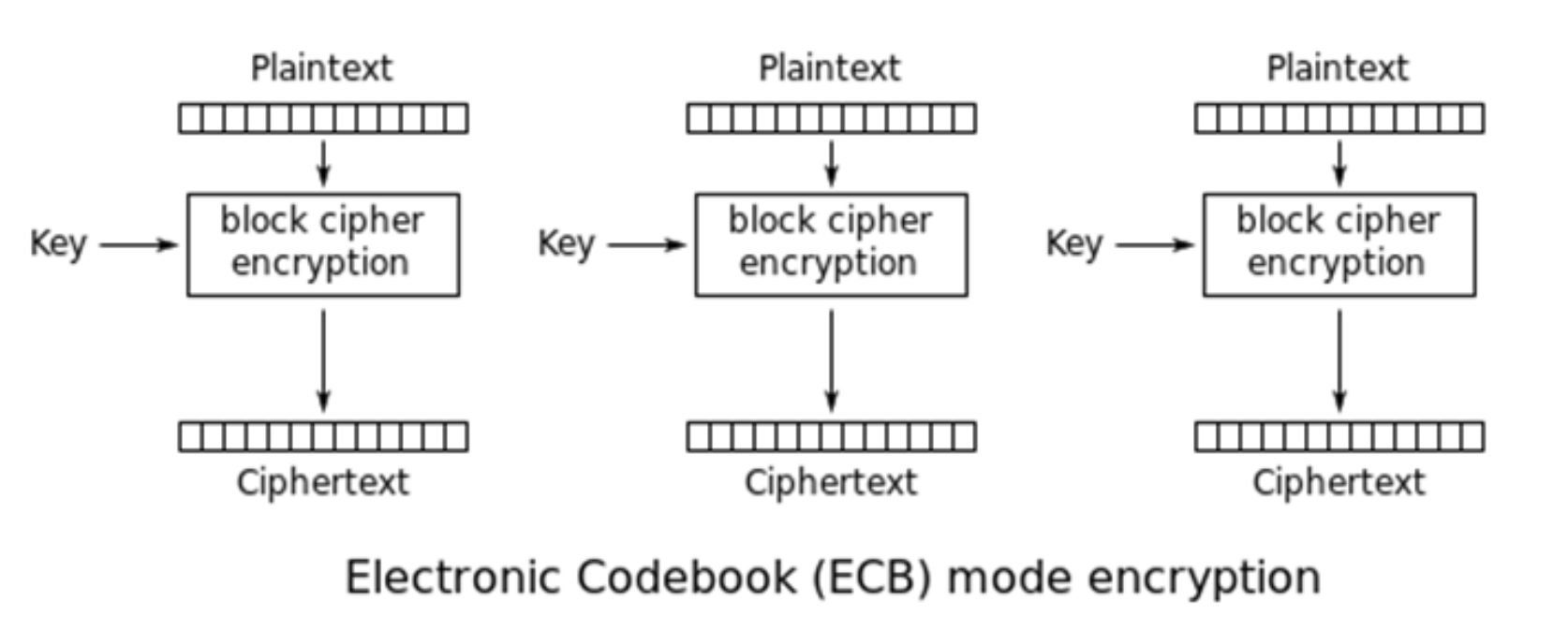
ECB

电子密码簿

将明文分块, 分别用一个 key进行加密.

• 优点: 加密和解密都可以并行进行.
• 缺点: 块内依旧存在可能相同的密文块.

CBC

Cipher Block Chaining 密文块链接模式

当前块的密文与前一块的密文有关:

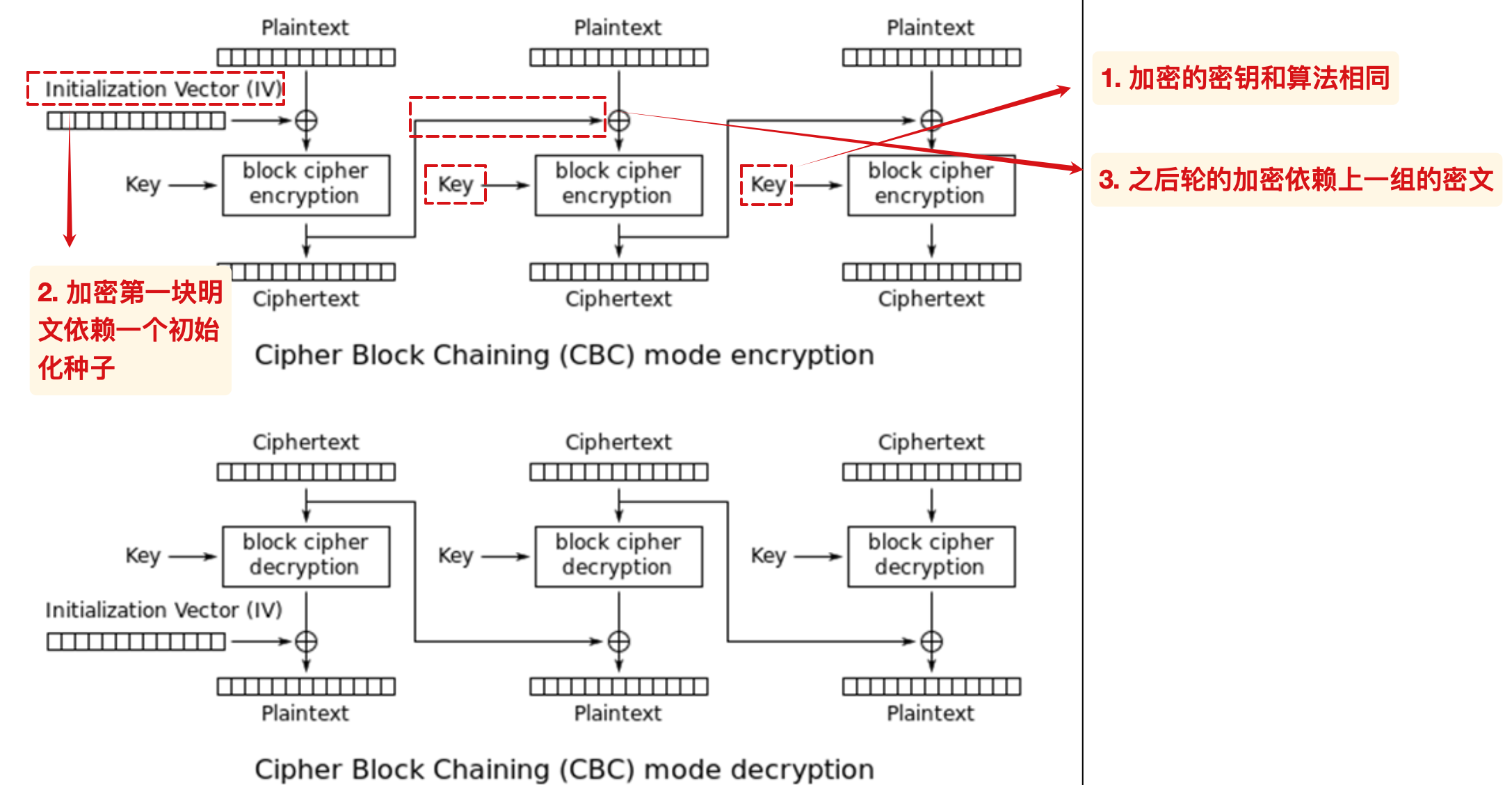
加密过程只能串行处理：

解密过程可以并行处理：

CFB

Cipher feedback 密文反馈模式

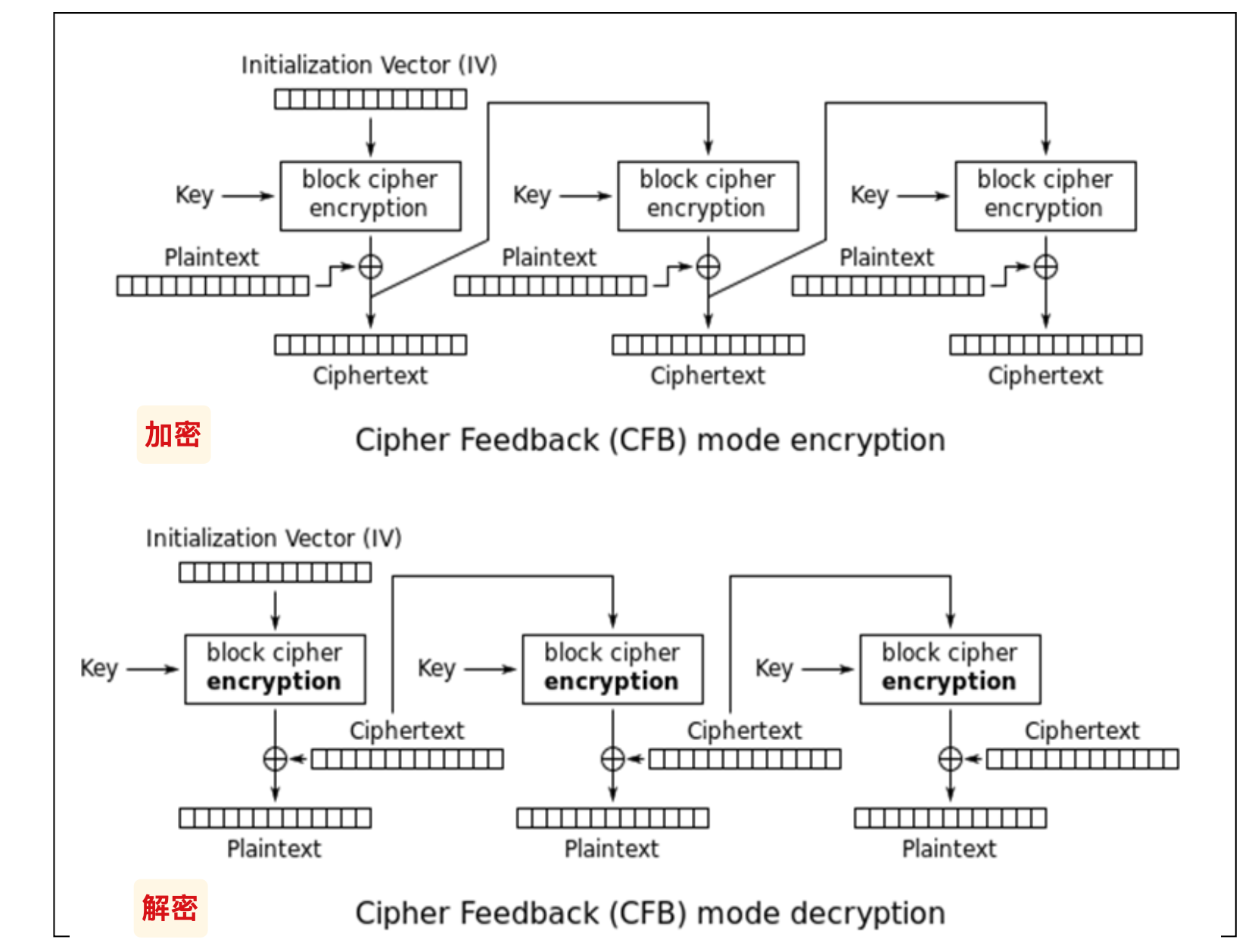
加密流程：

• 每次加密一个字节
  • 取X的高8位用E加密，然后与明文8位异或
• 然后每字节加密结束之后, 将 x 左移一个字节, 然后用 c[0]填充右侧;
• 循环上述, 注意每次都是用 x[0] 进行异或操作.

解密流程：

优点：

• 可以从密文传输的错误中恢复

RC4

是一种对称加密算算法，使用相同的密钥来加密和解密

结构体

typedef struct rc4_key
{
     unsigned char state[256];  // 256字节的状态表
     unsigned char x;          // 状态表索引x
     unsigned char y;          // 状态表索引y
} rc4_key;

密钥初始化

void prepare_key(unsigned char *key_data_ptr, int key_data_len, rc4_key *key)
{
   // 初始化状态表
   for(counter = 0; counter < 256; counter++)
      state[counter] = counter;
   
   // 使用密钥打乱状态表
   for(counter = 0; counter < 256; counter++)
   {
       index2 = (key_data_ptr[index1] + state[counter] + index2) % 256;
       swap_byte(&state[counter], &state[index2]);
       index1 = (index1 + 1) % key_data_len;
   }
}

key_data_ptr 为种子密钥；使用循环打乱state

加密/解密函数

void rc4(unsigned char *buffer_ptr, int buffer_len, rc4_key *key)
{
   for(counter = 0; counter < buffer_len; counter ++)
   {
      x = (x + 1) % 256;
      y = (state[x] + y) % 256;
      swap_byte(&state[x], &state[y]);
      xorIndex = (state[x] + state[y]) % 256;
      buffer_ptr[counter] ^= state[xorIndex];
   }
   key->x = x; /* 保存x及y这两个state的下标, 使得下次rc4()调用与本次调用可以衔接 */
   key->y = y;
}

示例

main()
{
   rc4_key k;
   char seed_key[] = "This is RC4 seed key.";
   char plaintext[100] = "A quick brown fox jumps over the lazy dog.";
   
   // 初始化密钥
   prepare_key(seed_key, strlen(seed_key), &k);
   
   // 加密
   rc4(buf, n, &k);
   
   // 解密（重新初始化密钥后再次加密）
   prepare_key(seed_key, strlen(seed_key), &k);
   rc4(buf, n, &k);
}

重要算法

DES

基本介绍

全称: Data Encryption Standard

流程示意图：

1. 明文的L/R中交替加密，每轮没有改变的部分与K参与计算，将结果用于改变另一部分
2. 64位的key去除8位（经过打乱）后变为56位的Key，然后将左右两侧分别循环左移，16次循环迭代中分别得到一组，然后利用56-48的表得到48位的值
3. 查询sbox得到32位的结果，与L异或

步骤解析

加密

L[i] = L[i-1] ^ f(K[i], R[i-1]);
R[i] = R[i-1]

其中的 f为：

long f(K[i], D[i]){
  K48 = shrink ( K[i]);
  D48 = expand( D[i]);
  return query_sbox(K48 ^ D48);
}

• shrink表示从最低位开始, 交替取用1/2次 比如 0,0,1,2,2,3…
• 为了将48位的数据展开成为数组, 我们将48位分为8组, 各组为 6bits 并且用 unsigned char来表示 —— unsigned char s[8].
  • s[i]仅仅使用低六位.
  • sbox恰好对应了8张表, 供 s进行查询, 且每次查询输入6位的输出是4位.
  • 因此, 8次查询的返回值一共是32位.

sbox的查询

由8个一维数组组成，分别对应48位分成的8组查询, 其中每个数组都是64位, 每行是0-15构成的不重复的16个数字, 共四行.

对于每组中的8位，实际的数据存储在低6位中，我们：

• 提取首尾的2-bit合成查询的行号；
• 提取中间的4-bit合成查询的列号

disturb

将输入的64位进行位重排 permutation

table中64字节是1～64的排序（因此内部的数值以1为基数）：

ip[0]=58 表示源数据中的第58位 ( 实际是第58-1=57位)要转化成目标数据中的第0+1=1 位

void disturb(unsigned char table[64], unsigned char s[8], unsigned char t[8])
{
   int i;
   byte_num, bit_num;
   /* memset(t, 0, sizeof(t)); 错误 */
   memset(t, 0, 8); /* 正确 */
   for(i=0; i<64; i++)
   {
      byte_num = (table[i]-1) / 8;
      bit_num = (table[i]-1) % 8;

// 如果对应的位是0，就直接进行下一轮的迭代，因为初始化t的各位都是0
      if(s[byte_num] & (0x80 >> bit_num)) /* 或 if(s[byte_num] & (0x01 << 7-bit_num)) */
         t[i/8] |= 0x80 >> i%8;
   }
}

• 每次循环取出table中的一个字节，并且通过 /8 与 %8的计算分别得到 byte_num, bit_num；
• 一共需要迭代64次，因为一共有8x8位需要替换

什么时候打乱？

• 明文在加密之前——ip
• 明文加密之后——fp
• sbox查询结果的32位数据）sbox_perm_table
  • 打乱之后再与“明文”异或
• 64位的密钥转换位56位 TODO——key_perm_table
• 56位的密钥循环左移之后取用48位 TODO

密钥的合成

56 2 48

   for (j=0; j<48; j++) /* select bits individually */
   {                    /* [%] Select 48 bits from 56 bits.
                               j is the target bit number, and 
                               key_56bit_to_48bit_table[j]-1 is 
                               the source bit number */
      /* check bit that goes to kn[j] */
      if (pcr[key_56bit_to_48bit_table[j]-1]) /* [%] pcr[key_56bit_to_48bit_table[j]-1] is SourceBit, j is TargetBit */
      {
         /* mask it in if it's there */
         b = j % 6;                     /*  same as bytebit[b+2] */
         kn[i][j/6] |= bytebit[b] >> 2; /* [%] remove the trailing 2 bits
                                           j=0    1    2    3    4    5
                                  bytebit[b]=0x80 0x40 0x20 0x10 0x08 0x04
                               bytebit[b]>>2=0x20 0x10 0x08 0x04 0x02 0x01
                                         */
      }
   } /* [%] for (j=0; j<48; j++) */
} /* [%] for (i=0; i<16; i++) */

此处的 bytebit为：

static int bytebit[8] = 
{
/* bit0  bit1  bit2  bit3  bit4  bit5  bit6  bit7 */
   0x80, 0x40, 0x20, 0x10, 0x08, 0x04, 0x02, 0x01
};

也就是8bit中从最左侧为1开始，不断右移知道最右侧为1

上述的 bytebit[b] >> 2 确保了1只可能只出现右侧的6位，因此实现了靠右对齐

6个为一组，构成8x6，i表示16轮迭代中的层数

操作汇总

利用一维idx在二维数组中索引

• 要求：给定1-64范围内的idx，在8x8 i.e. 8个字节中索引对应的1bit：
• 分析：
  • 8x8分别用3bit去索引

disturb中的实现

for(i=0; i<64; i++)
{
    byte_num = (table[i]-1) / 8;
    bit_num = (table[i]-1) % 8;

    // 如果对应的位是0，就直接进行下一轮的迭代，因为初始化t的各位都是0
    if(s[byte_num] & (0x80 >> bit_num)) /* 或 if(s[byte_num] & (0x01 << 7-bit_num)) */
        t[i/8] |= 0x80 >> i%8;
}

/ 8 等价于 >> 3 ； 同时 % 8等价于 &7

注意利用结果对二维的数组进行赋值（此处就是替换）：t[i/8] |= 0x80 >> i % 8

下面的实现也是合理的：

for (j=0; j<56; j++) /* convert key_perm_table to bits of key */
{                    /* [%] j is the target bit number of key */
   b = key_perm_table[j] - 1;   /* integer bit location */
                                /* [%] b is the source bit number of key, base 0 */
   m = b & 7;        /* [%] m = b % 8; */ /* find bit */ 

   pc1m[j]=(key[b>>3] & bytebit[m]) ? 1 : 0; /* find which key byte b is in */
                                             /* and which bit of that byte */
                                             /* and store 1-bit result */

}

不同于第一个实现，此处的pclm就是一个一维的数组，因此可以直接赋值。

构建反查表

已知sbox打乱表，需要根据表格内容构建反查表

• 先遍历取值范围
• 然后遍历已知表的idx，直到idx在已知表中索引得到的值与外层的遍历值相同
• 将外层的idx作为索引，用内层表的idx赋值给反查表

for(p=0; p<32; p++) /* [%] p=SourceBit */
{
   for(i=0; i<32; i++) /* [%] i=TargetBit */
   {
      if(sbox_perm_table[i]-1 == p) /* [%] sbox_perm_table[i] ranges within [1,32], so it is base 1, not base 0 */
      {
         sbox_perm_table_inverse[p] = i; /* [%] fill sbox_perm_table_inverse[p] with TargetBit=i */
         break;
      }
   }
}

循环右移与补偿

方法1：循环左移与右移：

// 循环左移n位
ulong ROL(ulong x, int n){
  n = n % 32;
	return (x << n) | (x >> ( 32 - n));
}

// 循环右移
ulong ROR(ulong x, int n){
  n = n % 32;
	return (x >> n) | (x << (32 - n));
}

方法2：循环右移一位的写法

// 循环右移，将r的最低位移到最高位，其他位向右移动一位
//  r & 1用于判断移位前的最低位是否为1，如果是，需要在循环右移的结果补偿
rt = (r >> 1) | ((r & 1) ? 0x80000000 : 0); /* [%] rt = ROR(rt, 1); */

循环左移

• 分别将左右两侧分为28bit进行循环左移；
• 用 b表示移位的位数，将pclm中的位赋值给pcr数组
• 注意在高28位中是 (j - 28 + xx) % 28 确保基数为1

for(j=0; j<28; j++) /* [%] left half */
{
   b = (j+key_rol_steps[i]) % 28;
   pcr[j] = pc1m[b];
}
for(j=28; j<56; j++) /* [%] right half */
{
   b = 28 + (j-28+key_rol_steps[i]) % 28;
   pcr[j] = pc1m[b];
}

转换为16进制

for(i=0; i<blocks*8; i++) // 转化成 16进制字符串
{
sprintf(hex+i*2, "%02X", bufout[i]); // 2表示最少2位，0表示不足填充0，X表示用大写的16进制输出
}

三重DES

由于存在一种称为中途相遇攻击（meet-in-the-middle attack）的技术，对双重DES加密构成了威胁，因此一般不使用双重DES，而是三重DES来多重加密

给定3个长度为56比特的密钥与明文 ，密文为：

中间的密钥采取解密的形式加密，仅仅是为了可以利用三重DES对单重DES加密的数据进行解密

AES

整体流程

• bytesub 字节代替变换
• shiftrows 行移位变换
• mixcolumns 列混淆变换

MixColumn

• 每次加密明文的一列.
• 3112为底,不断循环左移一位得到另一行.
  • 计算的时候是左列和右列诸位乘加. 和传统的矩阵乘法有所不同.
• 乘数的低位在前, 高位在后.

void MixColumn(unsigned char *p, unsigned char a[4], int do_mul)
{
   unsigned char b[4];
   unsigned char t[4][4];
   int j;
   for (j = 0; j < 4; j++)
   {
      get_column(p, j, b);            /* 从p所指矩阵m中提取第j列, 保存到数组b中. */
      if (do_mul)                     /* 在加密最后一轮以及解密第一轮的MixColumn步骤中不需要做乘法; */
         aes_polynomial_mul(a, b, b); /* 其余轮都要做乘法: b = a*b mod (X^4+1); */
      memcpy(t[j], b, 4);             /* 把乘法所得结果复制到t中第j行 */
   }
   memcpy(p, t, 4 * 4); /* 复制t中矩阵到p, 替换掉p中原有矩阵 */
}

对应的乘法：

// 有限域GF(2^8)多项式乘法 mod X^4 + 1
void aes_polynomial_mul(unsigned char x[4], unsigned char y[4], unsigned char z[4])
{
    unsigned char temp[8] = {0};
    int i, j;

    for (i = 0; i < 4; i++)
    {
        for (j = 0; j < 4; j++)
        {
            unsigned char product_coeff = aes_8bit_mul_mod_0x11B(x[3 - i], y[j]);
            temp[i + j] ^= product_coeff;
        }
    }
    z[0] = temp[0] ^ temp[4];
    z[1] = temp[1] ^ temp[5];
    z[2] = temp[2] ^ temp[6];
    z[3] = temp[3] ^ temp[7];
}

由于原先矩阵中的低次系数均在前，我们希望计算0～3次之间相乘的结果，因此在两层的嵌套中，采取 3-i 与 j 并举的方式；

i，j分别表示对应的阶数

密钥生成

流程概述：

1. 4i 形式比较特殊，一组（4x4字节）的key都在前者的基础上得到
2. 4i的计算流程：
   1. 4i 由 4i-1 临时赋值
   2. 循环左移1位
   3. 带入sbox替换查询
   4. 利用4i计算轮常数r
   5. 首字节与r异或
   6. 4i 与 4(i-1) 作异或得到最终的4I
3. 4i+1 = 4i ^ 4(i-1);
4. 4i+2 = 4i+1 ^ 4(i-1) + 1
5. …

pk[0] = pk[-1];
     rol_a_row(key + i * 4, 1);
     ByteSub(key + i * 4, 4);
     r = 1 << ((i - step) / step);

     // r较小的时候直接mod
     if (r <= 0x80)
        r = aes_8bit_mul_mod_0x11B(r, 1);
     else
        // r较大，为了避免处理大数，等价变换来优化
        r = aes_8bit_mul_mod_0x11B(r / 4, 4);
     key[i * 4] ^= r;
     pk[0] ^= pk[-step];

     for (j = 1; j < step; j++) /* i+j是密钥k的下标, 当(i+j)%step != 0时, */
     {                          /* k[i+j]只需做简单的异或处理 */
        if (...){}
  
        else /* 当(i+j)%step != 0时, k[i+j]只需做以下异或处理 */
           pk[j] = pk[j - step] ^ pk[j - 1];
     }
     pk += step;

最后两组的轮常数因为 mod 0x11B的缘故与的值并不相等

192和256位的密钥生成在上面的代码片段中被省略了

操作汇总

农夫算法

核心思想：通过被乘数的左移和乘数的右移，同时提前求模来加速计算

int p = 0 ;
for(int i = 0; i < 8 && x > 0 && y > 0; i++){
  if(y & 1){
    p ^= x;
  }
  y >>= 1;
  x <<= 1;
  
  // 通过迭代实现除法效果.
  if(x >= 0x100){
    x ^= 0x11B;  /* x = x % 0x11B */
  }
}

GF2的减法就是加法，加法也就是异或；多次异或直至结果小于0x100

RSA

属于公钥加密体制（非对称加密）

整体的流程：

1. 选择不等的素数
2. 计算
3. 选择与 互素的数
4. 计算在模下的乘法逆元
5. 公开公钥：
6. 保存私钥：

加密与解密：

Euler函数

• 定义： ：小于n且与n互素的整数的个数

• 对应的定理：

  特别的，如果是素数的话，有 = ，推知

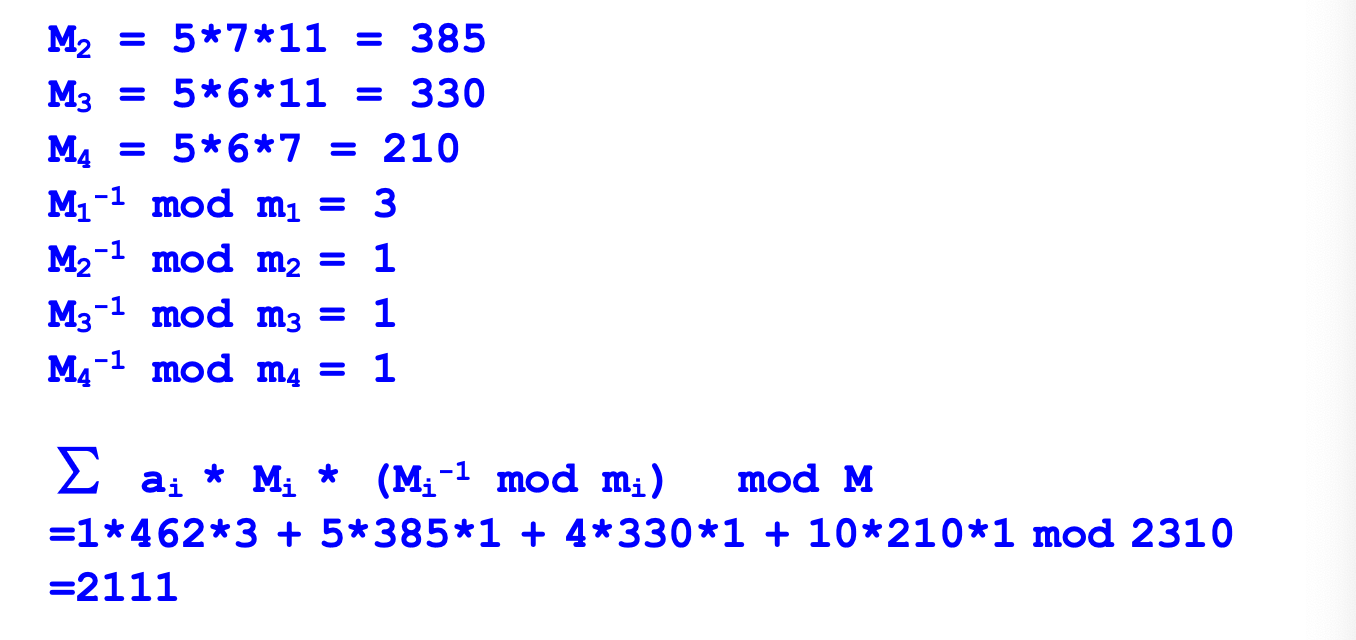
中国剩余定理

对于同余方程组：

其中 两两之间互素，并且令 ：

此时， 模 M的唯一解为：

其中逆元可以根据辗转相除法得到

e.g.

Euler函数的拓展性质

• 乘法性质：

  $$
  n_1, n_2 互素 \Longrightarrow \phi(n_1n_2) = \phi(n_1)\phi(n_2)
  $$

• 乘积公式：

  其中，且 为素数， 由对 的质因数分解得到

e.g.

签名

加密：A将一封信发送给B

• A将信件内容用B的公钥进行RSA的加密
• B收到内容后使用自己的私钥解密，得到的结果就是A信件的内容

签名：为了验证信件内容确实来自于A

• A对信件内容计算摘要，以MD5算法为例：M = MD5（L）
• 然后用A的私钥对M加密： M’ = RSA（M， A的私钥）
• A将M’与L一起发送给B
• B利用A的公钥计算 M‘’ = RSA（M’，A的公钥），同时计算MD5（L）
  • 如果后者的结果 = M‘’， 说明验证正确

注意A无法得到B的私钥，因此此处RSA加密解密涉及的都是A的密钥

ECC

直接参考pdf文档

常用ecc函数

注意0表示计算得到的y是偶数

补充

AES算法的明文长度和密文长度都是16字节，密钥长度分为16、24、32字节三种

请看调整后的表格，其中包含了ECC算法的特点：

算法	加密模式	明文-密文长度	密钥关系	备注
DES	ECB, CBC, CFB	明文64位，密文64位	64位密钥（实际56位用于加密，8位用于奇偶校验）	三重DES是为了对抗中途相遇攻击，增加安全性
AES	ECB, CBC, CFB (未在文中明确提及，但通常支持)	明文16字节，密文16字节	密钥长度可为16、24、32字节	具有字节代替、行移位、列混淆等变换
RSA	不适用（非对称加密算法）	明文长度需小于n，密文长度等于n	公钥(e,n)，私钥(d,n)； e与ϕ(n)互素，d为e模ϕ(n)的乘法逆元	基于大数分解的困难性；可用于加密和数字签名
ECC	不适用（非对称加密算法）	与所选椭圆曲线参数相关	基于椭圆曲线离散对数难题	相比RSA，在相同安全强度下密钥长度更短，计算效率更高

xgcd

/**
 * 扩展欧几里得算法实现
 * 计算gcd(x,y)以及x mod y的乘法逆元
 * 
 * @param x 第一个整数
 * @param y 第二个整数
 * @param pinverse 用于存储x mod y的乘法逆元的指针
 * @return 返回gcd(x,y)
 * 
 * 示例:
 * xgcd(3, 20, &inv)返回1，inv被赋值为7，因为3 * 7 ≡ 1 mod 20
 */
int xgcd(int x, int y, int *pinverse)
{
   // 初始化扩展欧几里得算法所需的变量
   // a1, b1用于跟踪第一个方程: x = a1*x + b1*y
   // a2, b2用于跟踪第二个方程: y = a2*x + b2*y
   int a1=1, b1=0, a2=0, b2=1;
   
   // q是商，r是余数
   int q, r, t;
   
   // n和old_n用于跟踪当前的被除数和除数
   int old_n;
   
   // 确保x <= y，如果不是则交换它们
   if(x > y)
   {
      t = x;
      x = y;
      y = t;
   }
   
   // 初始化n和r
   // n初始为较大的数y，r初始为较小的数x
   n = y;
   r = x;
   
   // 当余数r不为0时继续循环
   while(r != 0)
   {
      // 计算商q = n / r
      q = n / r;
  
      // 更新a1和a2的值
      // 这是扩展欧几里得算法的核心部分，同时计算系数
      t = a1;
      a1 = a2;
      a2 = t - q*a2;
  
      // 更新b1和b2的值
      t = b1;
      b1 = b2;
      b2 = t - q*b2;
  
      // 更新n和r的值，进行下一轮迭代
      t = n;
      n = r;
      r = t % r;
   }
   
   // 此时n就是gcd(x,y)
   // 但我们需要确保乘法逆元b1在模y下是正数
   // 因为b1可能是负数，所以加上y再取模y确保它在[0, y-1]范围内
   a1 = (a1+y) % y;  // 虽然a1是x的系数，但这里也确保它在模y下
   b1 = (b1+y) % y;  // 确保乘法逆元b1是正数
   
   // 将乘法逆元存入指针指向的变量
   *pinverse = b1;
   
   // 返回gcd(x,y)
   return n;
}